在金沙集团1862cc先导专项B、科技部国家重点研发计划、国家自然科学基金委员会、中国人民大学中央高校基本科研业务费专项资金、新基石研究员项目的资助下，金沙集团1862cc/北京凝聚态物理国家研究中心凝聚态理论与材料计算重点实验室T03组方辰研究员、翁红明研究员、方忠院士、博士后杨健（已出站）、博士研究生蒋毅（已毕业），宋子寅，朱天念以及中国人民大学刘正鑫教授，对自旋空间群的列举进行了系统的研究。他们完整列举了超过十五万个自旋空间群（包括共线、共面，以及非共面自旋空间群），并建立了一个自旋空间群在线数据库 https://cmpdc.iphy.ac.cn/ssg。该工作近日发表在《物理学评论X》（Physical Review X）上，文章链接 https://doi.org/10.1103/PhysRevX.14.031039。

　　在凝聚态物理中，对称性对于理解材料的物理性质有重要意义。对于具有平移对称性的晶体材料，只有 2、3、4和6重旋转操作是被允许的，加上镜面、空间反演等对称操作，人们发现共有230个不等价的空间群，用来描述三维晶体的对称性。而对于磁性晶体材料，磁性原子上带有非零的磁矩向量，产生了诸如铁磁、反铁磁、螺磁，乃至其他更复杂的磁构型。为了描述磁性材料的对称性，人们引入了磁空间群的概念。磁空间群将时间反演操作（翻转磁矩方向）与230个空间群的操作结合，共有1651个不等价的群。

　　然而，磁空间群要求其对称操作的实空间转动和自旋转动是绑定的，这样的限制导致其缺失了一类更精细的对称操作，即实空间和自旋解耦的操作。为了更完善的描述磁结构的对称性，人们引入了自旋空间群的概念。自旋空间群中，在满足构成群结构的前提下，空间和自旋转动可以任意组合，给出更加丰富的对称性，用来完整描述磁结构的对称性。

　　图1展示了该工作中列举自旋空间群的算法流程图。该工作系统列举了空间群12倍以内扩胞的所有自旋空间群，包括157289个非共面自旋群，24788个共面非共线自旋群，以及1421个共线自旋群。更高倍数扩胞的自旋空间群可以类似得到。所有自旋群的数据在数据库中可以方便的查询到。

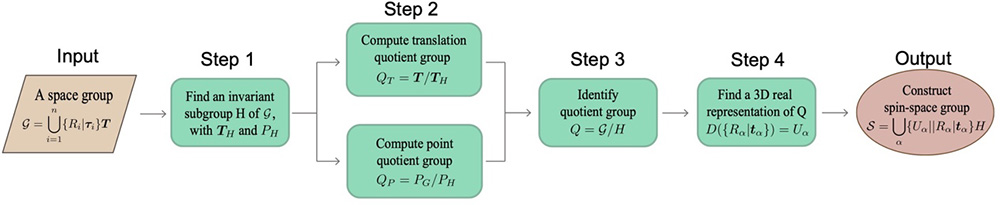
    图1：自旋空间群列举算法流程图。

　　自旋空间群的完整列举不仅可以更全面地描述磁结构，当材料的自旋-轨道耦合效应（SOC）较弱，或者相对于自旋劈裂较小时，自旋空间群可以用来描述电子结构的对称性。作为例子，图 2是磁性材料 Mn3Sn 的能带结构(a)和其在共面自旋空间群194.1.6.1.P 中的能带表示(b)：包括 GM 点的二维表示，A 点的四维表示，以及 GM-A 线上的三重简并点，这些高维简并点是被自旋空间群对称性保护的。注意到如果只考虑磁空间群对称性，这些高维简并点都属于偶然简并，无法用表示理论解释。因此，自旋空间群在理解磁性材料的电子结构方便具有很大优势。

    
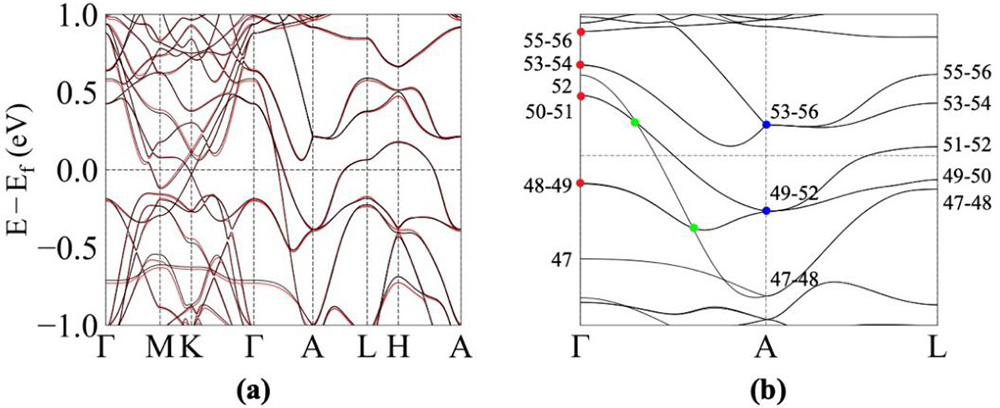
图2：磁性材料Mn3Sn 的能带结构及其表示。

　　与该工作同期发表在《物理学评论X》上的还有北京大学宋志达教授课题组【1】和南方科技大学刘奇航教授课题组【2】的工作，他们采用不同方法对自旋空间群也进行了系统列举，得到了相似的结果。三篇工作开启了磁性材料研究的新方向，我们试探性地称其为“自旋群磁性”。在自旋群磁性材料中，电子结构不是由自旋轨道耦合强度决定，而是由磁结构所具有的自旋空间群对称性决定。

参考文献：

1. https://doi.org/10.1103/PhysRevX.14.031037 

2. https://doi.org/10.1103/PhysRevX.14.031038 

文章链接：

https://doi.org/10.1103/PhysRevX.14.031039